Graphically this means that they have the same graph except that one is “flipped” or “reflected” through the line \(y=x\) as shown in Figure 4.5. First, let’s look at a graph of the log function with base e, that is: f(x) log e (x) (usually written ln x). \frac\) which as you probably know is often abbreviated \(\ln x\) and called the “natural logarithm” function.Ĭonsider the relationship between the two functions, namely, that they are inverses, that one “undoes” the other. The derivative of logs with base other than e.
Implicit and Logarithmic Differentiation. (ii) concave down on I if f (x) < 0 on the interval I. Let f be the second derivative of function f on a given interval I, the graph of f is (i) concave up on I if f (x) > 0 on the interval I. Derivatives of Exponential & Logarithmic Functions The sign of the second derivative informs us when is f increasing or decreasing. Simply stated, the derivative is the slope of drawdown data plotted on a graph with semilog axes (linear drawdown and logarithmic time). The second derivative of lnx is -1/x2 which is negative, therefore its graph is concave. Derivative Rules for Trigonometric Functions The graph y lnx of the function lnx is concave downward. Limits at Infinity, Infinite Limits and Asymptotes.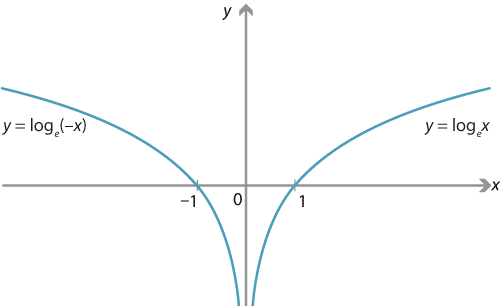 
Symmetry, Transformations and Compositions. Calculus Maximus Notes: 2.10 Log Functions. Derivatives Of Logarithmic Functions Logarithmic properties and formula for derivative of logarithms Find the derivative of the log function (Examples 1-2). The natural logarithm function is defined as an integral, and all other logarithmic functions are a multiple of it. 
Open Educational Resources (OER) Support: Corrections and Suggestions View Notes - NOTES 02.10 Derivatives of Log Functions & LOG DIFF from MATH 141E at Pennsylvania State University. Derivatives are the inverse of integrals.
0 kommentar(er)
